Картинка имеет форму прямоугольника со сторонами 24 см и 37 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 1440 см2. Какова ширина окантовки? Ответ дайте в сантиметрах.
Обозначим ширину окантовки как х.
Тогда ширина бумаги будет (2х+24) см (2х потому, что окантовка с обоих сторон от картинки).
Высока бумаги - (2х+37) см.
Sбумаги=(2х+37)(2х+24)=1440
4x2+48x+74x+888=1440
4x2+122x+888=1440
4x2+122x-552=0
x2+30,5x-138=0
Решим это
квадратное уравнение:
D=30,52-4*1*(-138)=930,25+552=1482,25
x1=(-30,5+38,5)/2=4
x2=(-30,5-38,5)/2=-34,5
Отрицательный ответ нам не подходит, следовательно, ширина окантовки 4 см.
Ответ: 4
Поделитесь решением
Присоединяйтесь к нам...
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=19, а расстояние от точки K до стороны AB равно 7.
Сторона ромба равна 32, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Тангенс острого угла прямоугольной трапеции равен 2/9. Найдите её большее основание, если меньшее основание равно высоте и равно 54.
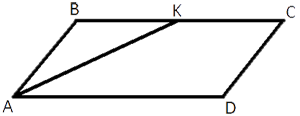Сторона BC параллелограмма ABCD вдвое больше стороны AB.
Точка K — середина стороны BC. Докажите, что AK — биссектриса
угла BAD.
Укажите номера верных утверждений.
1) Любой квадрат является ромбом.
2) Против равных сторон треугольника лежат равные углы.
3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: