Решите систему уравнений
x2=4y+1
x2+3=4y+y2
В первом уравнении x2=4y+1, подставим это значение x2 во второе уравнение:
(4y+1)+3=4y+y2
4y+1+3=4y+y2
0=4y+y2-4y-4
y2-4=0
Можно решить это
квадратное уравнение через
дискриминант, но в данном случае можно проще:
y2-4=0
y2-22=0
(y-2)(y+2)=0
Произведение равно нулю, когда один из множителей равен нулю:
1) y-2=0 => y1=2
2) y+2=0 => y2=-2
Найдем x:
1) Когда y=2,
x2=4*2+1
x2=9
x2-9=0
x2-32=0
(x-3)(x+3)=0
x1=3
x2=-3
2) Когда y=-2
x2=4*(-2)+1
x2=-8+1
x2=-7
Данное уравнение не имеет решений, так как квадрат любого числа имеет положительное значение.
Ответ: (3;2) и (-3;2)
Поделитесь решением
Присоединяйтесь к нам...
Расстояние от Солнца до Нептуна свет проходит примерно за 252,95 минуты. Найдите приблизительно расстояние от Солнца до Нептуна, ответ округлите до миллионов км. Скорость света равна 300000 км/с.
Расстояние между пристанями А и В равно 126 км. Из А в В по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот проплыл 36 км. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 4 км/ч.
Масштаб карты 1:100000. Чему равно расстояние между городами A и B (в км), если на карте оно составляет 1,5 см?
Решите систему уравнений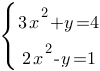 
Решите неравенство:
14/(x2+2x-15)≤0
.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: