Укажите решение неравенства 7x-x2<0.
1) 
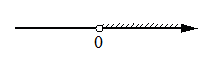
2) 
3) 
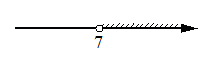
4) 
Чтобы решить это неравенство надо найти корни соответствующего уравнения:
7x-x2=0
Можно решить это квадратное уравнение через дискриминант, но в данном случае можно поступить проще:
x(7-x)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому рассмотрим два случая:
1) x1=0
2) 7-x=0 => x2=7
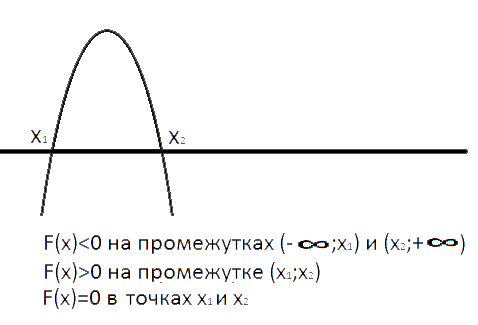Теперь рассмотрим график нашей функции - это парабола.
Так как коэффициент при x2 равен -1, т.е. отрицательный, то ветви параболы направлены вниз.
Нас интересует диапазон, где наша функция меньше нуля (по условию). Это означает, что нас интересует только тот диапазон (или диапазоны), где график функции располагается под осью Х.
В нашем случае, график находится под осью на диапазонах от -∞ до x1 и от x2 до +∞.
x1 и x2 - это корни, которые мы нашли ранее.
(-∞;0)∪(7;+∞)
Это соответствует рисунку:
Ответ: 1)
Поделитесь решением
Присоединяйтесь к нам...
На координатной прямой отмечено число a.
Из следующих утверждений выберите верное.
1) (a-6)2>1
2) (a-7)2>1
3) a2>36
4) a2>49
Решение какого из данных неравенств изображено на рисунке?
1) x2-7x<0
2) x2-49>0
3) x2-7x>0
4) x2-49<0
Решите уравнение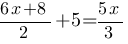 
На каком рисунке изображено множество решений неравенства x2-4x+3≥0?
1) 
2) 
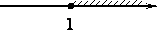
3) 
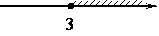
4) 
Решите уравнение x(x2+6x+9)=4(x+3).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: