Решите уравнение x(x2+6x+9)=4(x+3).
Если внимательно посмотреть на уравнение, то можно заметить, что скобка в левой части представляет из себя квадрат суммы:
x(x2+6x+32)=4(x+3)
x(x+3)2=4(x+3)
x(x+3)2-4(x+3)=0
Вынесем за общую скобку (x+3):
(x+3)(x(x+3)-4)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому приравняем каждую скобку к нулю и найдем решения:
1) x+3=0 => x1=-3
2) x(x+3)-4=0
x2+3x-4=0
Решим это квадратное уравнение через дискриминант:
D=32-4*1*(-4)=9+16=25
x2=(-3+5)/(2*1)=2/2=1
x3=(-3-5)/(2*1)=-8/2=-4
Ответ: x1=-3, x2=1, x3=-4
Поделитесь решением
Присоединяйтесь к нам...
Укажите решение неравенства
2x-x2≤0
1) (-∞;0]∪[2;+∞)
2) [0;+∞)
3) [2;+∞)
4) [0;2]
Плата за телефон составляет 310 рублей в месяц. В следующем году она увеличится на 13%. Сколько рублей придётся платить ежемесячно за телефон в следующем году?
Решите неравенство: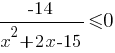 
В начале года число абонентов телефонной компании «Восток» составляло 500 тыс. человек, а в конце года их стало 575 тыс. человек. На сколько процентов увеличилось за год число абонентов этой компании?
Решите систему неравенств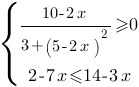 
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: