
Расстояние между пристанями А и В равно 126 км. Из А в В по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот проплыл 36 км. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 4 км/ч.
Для начала определим, что есть общего у у обоих транспортных средств (у лодки и плота).
Расстояние они прошли разное.
Скорости у них разные и нет зависимости одной от другой.
Время в пути у них разное, но известна зависимость. Из условия известно, что лодка была в пути на 1 час меньше, т.е.:
tl+1=tp
Выразим время лодки и плота через расстояние и время.
Лодка проплыла по течению 126 км, т.е. скорость лодки относительно берега = собственная скорость лодки (vl) + скорость реки (vr).
Против течения лодка проплыла тоже 126 км, но теперь скорость лодки относительно берега = собственная скорость лодки (vl) - скорость реки (vr).
Тогда получаем такое равенство:
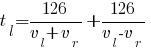
Для плота все проще, его скорость равна скорости реки (vr), а рассояние, которое он прошел = 36 км.
Для времени плота получаем такое равенство:
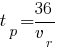
Подставляем в первое равенство:
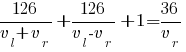
Подставляем известные значения:
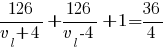
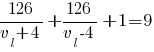
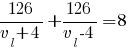
Приводим к общему знаменателю:
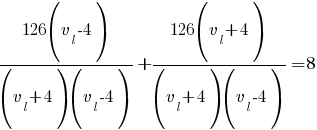
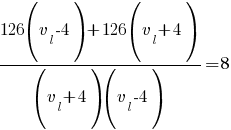
В числителе раскрываем скобки, а в знаменателе применим формулу
разность квадратов:
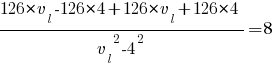
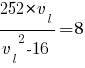
252*vl=8(vl2-16) |:4
63*vl=2(vl2-16)
63*vl=2vl2-32
0=2vl2-63*vl-32
Решим это квадратное уравнение через дискриминант:
D=(-63)2-4*2*(-32)=3969+256=4225
1) vl=(-(-63)+65)/(2*2)=(63+65)/4=32
2) vl=(-(-63)-65)/(2*2)=(63-65)/4=-0,5
Так как скорость не может быть отрицательной, то vl=32 км/ч.
Ответ: 32
Поделитесь решением
Присоединяйтесь к нам...
На координатной прямой отмечено число a.

Расположите в порядке возрастания числа a-1, 1/a, a.
1) a-1, 1/a, a
2) a, 1/a, a-1
3) a-1, a, 1/a
4) a, a-1, 1/a
Расстояние между двумя пристанями по реке равно 24 км. Моторная лодка прошла от одной пристани до другой, сделала стоянку на 1 ч 40 мин и вернулась обратно. Всё путешествие заняло 6 целых и 2/3 ч. Найдите скорость течения реки, если известно, что скорость моторной лодки в стоячей воде равна 10 км/ч.
Решите уравнение x2=5x.
Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Укажите решение неравенства 5x-2(2x-8)<-5.
1) (-∞;11)
2) (11;+∞)
3) (-∞;-21)
4) (-21;+∞)
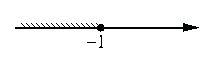
Укажите решение неравенства
(x+1)(x-6)≤0.
1) 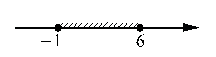
2) 
3) 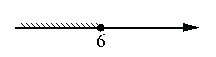
4) 
Комментарии: