Решите уравнение x2-3x+√3-x=√3-x+10
Так как в уравнении присутствует корень, то нужно выписать Область Допустимых значений (ОДЗ).
Значение под корнем не может быть отрицательным, следовательно:
3-x≥0
3≥x
Теперь вернемся к нашему уравнению и перенесем все в левую часть:
x2-3x+√3-x-√3-x-10=0
x2-3x-10=0
Решим это квадратное уравнение через дискриминант:
D=(-3)2-4*1*(-10)=9+40=49
x1=(-(-3)+7)/(2*1)=(3+7)/2=5
x2=(-(-3)-7)/(2*1)=(3-7)/2=-2
Проверяем ОДЗ: 3≥x. Т.е. x=5 - не подходит.
Ответ: -2
Поделитесь решением
Присоединяйтесь к нам...
Укажите решение системы неравенств
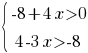
1) нет решений
2) (-∞;4)
3) (2;+∞)
4) (2;4)
Решите систему уравнений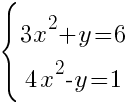 
На каком рисунке изображено множество решений системы неравенств
x-4≥0,
x-0,3≥1?
1) 
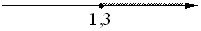
2) 
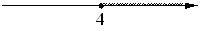
3) 
4) 
Решите уравнение -3x2+5x-3=-x2+3x+(2-2x2).
Решите систему неравенств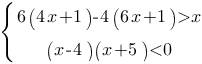 
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: