Решите неравенство 2x-x2<0.
Для решения неравенства найдем корни уравнения 2x-x2=0
Можно это квадратное уравнение решить через дискриминант, но в данном случае легче решить по другому:
Выносим за скобки х:
x(2-x)=0
Произведение равняется нулю, когда один из множителей равен нулю, поэтому рассмотрим два варианта:
1) x1=0
2) 2-x=0 => x2=2
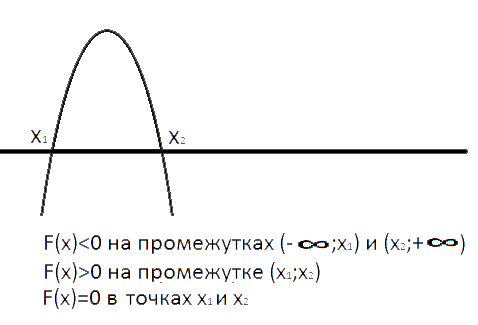График функции 2x-x2 представляет из себя параболу. Коэффициен "а" равен -1, т.е. меньше нуля, поэтому ветви параболы направлены вниз, как на рисунке. График пересекает ось Х в точках x1 и x2.
2x-x2 меньше 0, когда график располагается ниже оси Х, т.е. на диапазонах (-∞;0) и (2;+∞)
Ответ: (-∞;0)∪(2;+∞)
Поделитесь решением
Присоединяйтесь к нам...
Укажите неравенство, решение которого изображено на рисунке.
1) x2-49>0
2) x2-49<0
3) x2+49<0
4) x2+49>0
Моторная лодка прошла против течения реки 77 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 4 км/ч.
Расстояние между двумя пристанями по реке равно 24 км. Моторная лодка прошла от одной пристани до другой, сделала стоянку на 1 ч 40 мин и вернулась обратно. Всё путешествие заняло 6 целых и 2/3 ч. Найдите скорость течения реки, если известно, что скорость моторной лодки в стоячей воде равна 10 км/ч.
Решите неравенство 
Два автомобиля отправляются в 420-километровый пробег. Первый едет со скоростью на 24 км/ч большей, чем второй, и прибывает к финишу на 2 ч раньше второго. Найдите скорость первого автомобиля.
Хочу получать новые решения
Ни какого спама
Автор: Таська
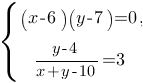
Комментарии: