
Укажите неравенство, которое не имеет решений.
1) x2-8x-83>0
2) x2-8x+83<0
3) x2-8x-83<0
4) x2-8x+83>0
Неравенство не имеет решений, когда не найдется ни одного такого значения "х", при котором неравенство было бы верно.
Для этого соответствующее равенство должно не иметь корней.
Найдем дискриминант для каждого
квадратного уравнения:
1) x2-8x-83=0
D=(-8)2-4*1*(-83)=64+332=396
Этот дискриминант больше нуля, следовательно уравнение имеет два корня. Т.е. неравенство 1) будет иметь решение.
2) x2-8x+83=0
D=(-8)2-4*1*83=64-332=-268
Этот дискриминант меньше нуля, т.е. это уравнение не имеет корней.
3) Уравнение совпадает с 1).
4) Уравнение совпадает с 2).
Осталось выбрать между двумя неравенствами:
2) x2-8x+83<0
и
4) x2-8x+83>0
Будем рассуждать логически, коэффициент при x2 равен 1, т.е. больше нуля. Следовательно график этой функции - парабола с ветвями, направленными вверх. Вверх ветви уходят в бесконечность (в +∞), т.е. чтобы график не пересекал ось Х, он должен быть целиком выше оси Х. Т.е.:
x2-8x+83>0 - верно при любом "х".
И наоборот, x2-8x+83<0 - не верно ни при каком "х", т.е. не имеет решений.
Ответ: 2)
Поделитесь решением
Присоединяйтесь к нам...
Решите неравенство 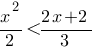
Найдите корень уравнения 8+7x=9x+4.
На пост председателя школьного совета претендовали два кандидата. В голосовании приняли участие 70 человек. Голоса между кандидатами распределились в отношении 3:7. Сколько голосов получил победитель?
Свежие фрукты содержат 80% воды, а высушенные — 28%. Сколько требуется свежих фруктов для приготовления 80 кг высушенных фруктов?
Расстояние между пристанями А и В равно 48 км. Из А в В по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошёл 25 км. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 5 км/ч.
Комментарии: