Два автомобиля одновременно отправляются в 560-километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 1 ч раньше второго. Найдите скорость первого автомобиля.
Обозначим:
v - скорость первого автомобиля.
v-10 - скорость второго автомобиля.
t - время первого автомобиля.
t+1 - время второго автомобиля.
Получаем два уравнения:
v*t=560 - для первого автомобиля.
(v-10)(t+1)=560 - для второго автомобиля.
Выразим t через v в первом уравнении:
t=560/v
И подставим его во второе уравнение:
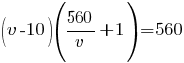
Раскроем скобки:
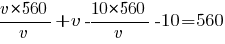
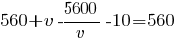
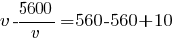
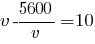
Умножим все уравнение на v:
v2-5600=10v
v2-10v-5600=0
Решим это квадратное уравнение через дискриминант:
D=(-10)2-4*1*(-5600)=100+22400=22500
v1=(-(-10)+150)/(2*1)=(10+150)/2=160/2=80
v2=(-(-10)-150)/(2*1)=(10-150)/2=-140/2=-70
Так как скорость не может быть отрицательной, то остается только один вариант.
Ответ: 80
Поделитесь решением
Присоединяйтесь к нам...
Решите систему уравнений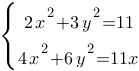 
Решите систему уравнений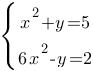 
На каком из рисунков изображено решение неравенства 81x2<16?
1) 
2) 
3) 
4) 
Рыболов проплыл на лодке от пристани некоторое расстояние вверх по течению реки, затем бросил якорь, 2 часа ловил рыбу и вернулся обратно через 5 часов от начала путешествия. На какое расстояние от пристани он отплыл, если скорость течения реки равна 2 км/ч, а собственная скорость лодки 6 км/ч?
Два велосипедиста одновременно отправляются в 60-километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: