
Решите неравенство 2x-x2<0.
Для решения неравенства найдем корни уравнения 2x-x2=0
Можно это квадратное уравнение решить через дискриминант, но в данном случае легче решить по другому:
Выносим за скобки х:
x(2-x)=0
Произведение равняется нулю, когда один из множителей равен нулю, поэтому рассмотрим два варианта:
1) x1=0
2) 2-x=0 => x2=2
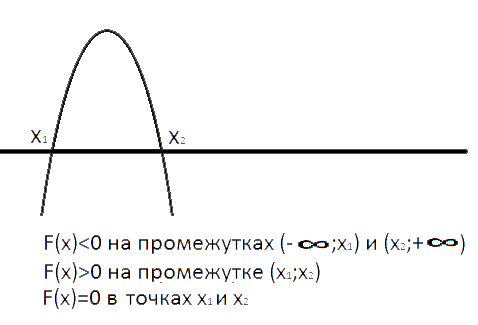 График функции 2x-x2 представляет из себя параболу. Коэффициен "а" равен -1, т.е. меньше нуля, поэтому ветви параболы направлены вниз, как на рисунке. График пересекает ось Х в точках x1 и x2.
График функции 2x-x2 представляет из себя параболу. Коэффициен "а" равен -1, т.е. меньше нуля, поэтому ветви параболы направлены вниз, как на рисунке. График пересекает ось Х в точках x1 и x2.
2x-x2 меньше 0, когда график располагается ниже оси Х, т.е. на диапазонах (-∞;0) и (2;+∞)
Ответ: (-∞;0)∪(2;+∞)
Поделитесь решением
Присоединяйтесь к нам...
Решите неравенство 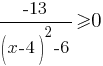
Решите уравнение 3x2=9x.
Если уравнение имеет более одного корня, в ответ запишите меньший
из корней.
Решите уравнение -3x2+x+9=-x2-4x+(-2-2x2).
На пост председателя школьного совета претендовали два кандидата. В голосовании приняли участие 70 человек. Голоса между кандидатами распределились в отношении 3:7. Сколько голосов получил победитель?
Решите неравенство 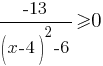
Комментарии: