
Решите уравнение (x2-9)2+(x2-2x-15)2=0.
Вариант №1 (Предложил пользователь Людмила)
Это равенство будет выполняться тогда и только тогда, когда x2-9=0 и
x2-2x-15=0.
Пояснение: оба этих слагаемых возведены в квадрат, следовательно, будут всегда положительные. А сумма двух положительный чисел может быть равна нулю только, когда эти оба числа равны нулю.
Получаем систему уравнений:
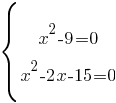
Решим по отдельности каждое уравнение, а одинаковые корни этих уравнений и будут решением системы.
1) x2-9=0
Можно решить это
квадратное уравнение через
дискриминант, но в данном случае выберем путь проще, воспользуемся формулой разность квадратов:
x2-32=0
(x-3)(x+3)=0
Произведение равно нулю, когда один из множителей равен нулю:
x-3=0 => x1=3
x+3=0 => x2=-3
2) x2-2x-15=0
Решим это квадратное уравнение через
дискриминант:
D=(-2)2-4*1*(-15)=4+60=64
x1=(-(-2)+8)/(2*1)=(2+8)/2=5
x2=(-(-2)-8)/(2*1)=(2-8)/2=-3
Для обоих уравнений x=-3 является общим корнем, это и есть решение системы и первоначального уравнения.
Ответ: -3
Поделитесь решением
Присоединяйтесь к нам...
На координатной прямой отмечено число a.

Найдите наибольшее из чисел a2, a3, a4.
На координатной прямой отмечено число a.

Найдите наибольшее из чисел a2, a3, a4.
1) a2
2) a3
3) a4
4) не хватает данных для ответа
Рыболов проплыл на лодке от пристани некоторое расстояние вверх по течению реки, затем бросил якорь, 2 часа ловил рыбу и вернулся обратно через 5 часов от начала путешествия. На какое расстояние от пристани он отплыл, если скорость течения реки равна 4 км/ч, а собственная скорость лодки 6 км/ч?
На координатной прямой отмечено число a.

Найдите наименьшее из чисел a2, a3, a4.
1) a2
2) a3
3) a4
4) не хватает данных для ответа
Решите неравенство (x-3)(2x+3)<-7.
Комментарии:
(2017-05-14 18:46:56) Администратор: Людмила, спасибо за подсказку. Я опубликовал Ваш вариант решения от Вашего имени.
(2017-05-13 18:37:51) Людмила: Опять сложное решение. (x2-9)2+(x2-2x-15)2=0 тогда и только тогда, когда x2-9=0 и x2-2x-15=0. Далее решается система этих уравнений