
Укажите номера верных утверждений.
1) Центр описанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
2) Квадрат является прямоугольником.
3) Сумма углов любого треугольника равна
180°.
Рассмотрим каждое утверждение:
1) "Центр описанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника".
Высота, проведенная к основанию является и
медианой, и биссектрисой (по
свойству равнобедренного треугольника), т.е. является
серединным перпендикуляром. А центром описанной окружности является точка пересечения
серединных перпендикуляров (
теорема об описанной окружности). Следовательно, это утверждение верно.
2) "Квадрат является прямоугольником", это утверждение верно (по
определению).
3) "Сумма углов любого треугольника равна 180°", это утверждение верно (по
теореме).
Поделитесь решением
Присоединяйтесь к нам...
 ABCDEFGHI – правильный девятиугольник. Найдите угол ADC. Ответ дайте в градусах.
ABCDEFGHI – правильный девятиугольник. Найдите угол ADC. Ответ дайте в градусах.
 На стороне AB треугольника ABC взята точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=12, BC=18 и CD=8.
На стороне AB треугольника ABC взята точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=12, BC=18 и CD=8.
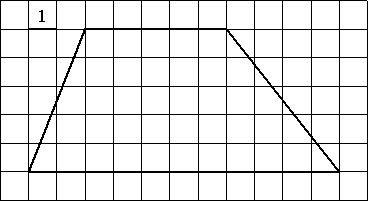 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
 Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
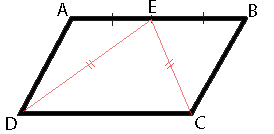 В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм - прямоугольник.
В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм - прямоугольник.
Комментарии: