
 Радиус окружности, описанной около равностороннего треугольника, равен 12. Найдите высоту этого треугольника.
Радиус окружности, описанной около равностороннего треугольника, равен 12. Найдите высоту этого треугольника.
По
первому свойству равностороннего треугольника, все его углы равны 60°.
По
теореме синусов:
2R=a/sin60
a=2R*sin60= (найдем sin60 по таблице)
=2*12*√3/2=12√3
По второму свойству равностороннего треугольника, высота равна:
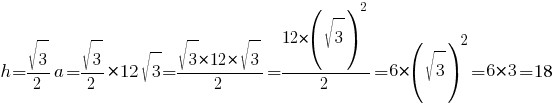
Ответ: 18
Поделитесь решением
Присоединяйтесь к нам...
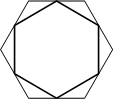 Дан правильный шестиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный шестиугольник.
Дан правильный шестиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный шестиугольник.
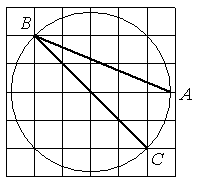 Найдите угол ABC. Ответ дайте в градусах.
Найдите угол ABC. Ответ дайте в градусах.
 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
 В треугольнике АВС углы А и С равны 30° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
В треугольнике АВС углы А и С равны 30° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
 В трапеции ABCD AD=8, BC=5, а её площадь равна 13. Найдите площадь треугольника ABC.
В трапеции ABCD AD=8, BC=5, а её площадь равна 13. Найдите площадь треугольника ABC.
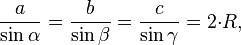 ,
,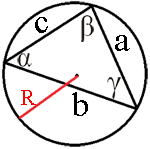
Комментарии: