
 В треугольнике АВС углы А и С равны 30° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
В треугольнике АВС углы А и С равны 30° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
По
теореме о сумме углов треугольника:
180°=∠A+∠B+∠C
∠B=180°-∠A-∠C=180°-30°-50°=100°.
∠ABD=∠B/2=100°/2=50° (т.к. BD -
биссектриса).
Рассмотрим треугольник BHC.
По
теореме о сумме углов треугольника:
180°=∠CHB+∠C+∠CBH=50°+90°+∠CBH
∠CBH=180°-50°-90°=40°.
Тогда искомый угол ∠DBH=∠B-∠ABD-∠CBH=100°-50°-40°=10°.
Ответ: 10
Поделитесь решением
Присоединяйтесь к нам...
 Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 60, тангенс угла BAC равен 5/12. Найдите радиус окружности, вписанной в треугольник ABC.
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 60, тангенс угла BAC равен 5/12. Найдите радиус окружности, вписанной в треугольник ABC.
 Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=12 и MB=18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=12 и MB=18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
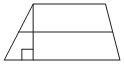 Основания трапеции равны 2 и 6, а высота равна 3. Найдите среднюю линию этой трапеции.
Основания трапеции равны 2 и 6, а высота равна 3. Найдите среднюю линию этой трапеции.
Косинус острого угла A треугольника ABC равен 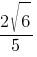 . Найдите sinA.
. Найдите sinA.
 На отрезке AB выбрана точка C так, что AC=12 и BC=3. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
На отрезке AB выбрана точка C так, что AC=12 и BC=3. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
Комментарии: