
Выписаны первые несколько членов геометрической прогрессии: -256; 128; -64; … Найдите сумму первых семи её членов.
В
геометрической прогрессии зависимость членов прогрессии можно записать так: bn+1=bnq
Тогда:
b2=b1q
128=-256q
q=128/(-256)=-1/2=-0,5
Сумму первых семи членов
геометрической прогрессии можно вычисли по формуле или "в лоб", вычислив недостающие члены прогрессии и сложить их:
1) По формуле:
S7=(b1(1-q7))/(1-q)
S7=(-256(1-(-0,5)7))/(1-(-0,5))=(-256(1-(-0,0078125)))/(1+0,5)=-258/1,5=-172
2) "В лоб":
b1=-256
b2=128
b3=-64
b4=b3q=-64*(-0,5)=32
b5=b4q=32*(-0,5)=-16
b6=b5q=(-16)*(-0,5)=8
b7=b6q=8*(-0,5)=-4
S7=-256+128+(-64)+32+(-16)+8+(-4)=-172
Ответ: -172
Поделитесь решением
Присоединяйтесь к нам...
Последовательность (bn) задана условиями: b1=4, 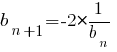
Найдите b3.
Дана арифметическая прогрессия: 1; 3; 5; … . Найдите сумму первых семидесяти её членов.
Геометрическая прогрессия задана условием bn=62,5*2n. Найдите сумму первых её 4 членов.
Геометрическая прогрессия задана условиями b1=-1, bn+1=2bn. Найдите b7.
Дана арифметическая прогрессия: -6; -3; 0; … Найдите сумму первых сорока её членов.
Комментарии:
(2020-05-15 10:16:22) Администратор: Анна, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и мы ее обязательно добавим.
(2020-05-07 19:22:12) анна: в геом прогрессии b1=1/4 q=1/2 bn=1/256 найти n 8