
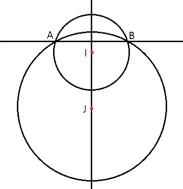
 Окружности с центрами в точках I и J пересекаются в точках A и B, причём точки I и J лежат по одну сторону от прямой AB. Докажите, что AB⊥IJ.
Окружности с центрами в точках I и J пересекаются в точках A и B, причём точки I и J лежат по одну сторону от прямой AB. Докажите, что AB⊥IJ.
AB - является
хордой для обоих окружностей.
По
второму свойству хорды,
серединный перпендикуляр
хорды проходит через центр обеих окружностей.
А так как через две точки можно провести только одну прямую, то
серединный перпендикуляр и есть прямая IJ.
Т.е. IJ перпендикулярна AB.
Поделитесь решением
Присоединяйтесь к нам...
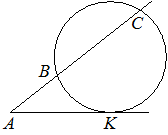 Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=6, AC=54. Найдите AK.
Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=6, AC=54. Найдите AK.
 Площадь прямоугольного треугольника равна 882√
Площадь прямоугольного треугольника равна 882√
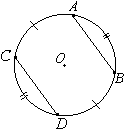
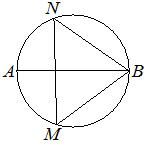 На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=36°. Найдите угол NMB. Ответ дайте в градусах.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=36°. Найдите угол NMB. Ответ дайте в градусах.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника COD.
 Сторона ромба равна 32, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Сторона ромба равна 32, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?

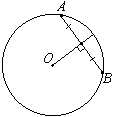
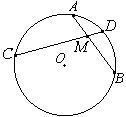
Комментарии:
(2016-01-05 15:59:33) Дима: Спасибо!!!