
 Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 46° и 35° соответственно. Ответ дайте в градусах.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 46° и 35° соответственно. Ответ дайте в градусах.
По свойству
равнобедренной трапеции - углы при основании равны.
Тогда ∠ADC=46°+35°=81°.
Сумма углов четырехугольника равна 360°, тогда получаем, что:
360°=81°+81°+∠DCB+∠CBA,
∠DCB+∠CBA=360°-81°-81°=198°, а учитывая, что ∠DCB=∠CBA (по тому
свойству равнобедренной трапеции), получаем ∠DCB=∠CBA=198°/2=99°, эти углы и есть бОльшие в трапеции
Ответ: 99
Поделитесь решением
Присоединяйтесь к нам...
 Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=2, а расстояние от точки K до стороны AB равно 1.
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=2, а расстояние от точки K до стороны AB равно 1.
 Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB=20, CD=48, а расстояние от центра окружности до хорды AB равно 24.
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB=20, CD=48, а расстояние от центра окружности до хорды AB равно 24.
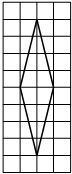 На клетчатой бумаге с размером клетки 1x1 изображён ромб. Найдите площадь этого ромба.
На клетчатой бумаге с размером клетки 1x1 изображён ромб. Найдите площадь этого ромба.
 В треугольнике ABC проведена биссектриса AL, угол ALC равен 152°, угол ABC равен 137°. Найдите угол ACB. Ответ дайте в градусах.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 152°, угол ABC равен 137°. Найдите угол ACB. Ответ дайте в градусах.
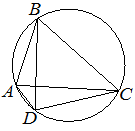 Четырёхугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах.
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах.
Комментарии: