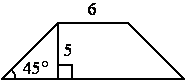В равнобедренной трапеции известны высота, меньшее основание и угол при основании. Найдите большее основание.
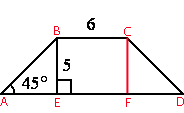Проведем
высоту CF.
Рассмотрим треугольники ABE и DCF.
∠BAE=∠CDF=45° (по
свойству равнобедренной трапеции).
∠BEA=∠CFD=90° (так как BE и CF -
высоты).
Используя
теорему о сумме углов треугольника, получаем, что:
∠EBA=∠FCD
AB=CD (по
определению равнобедренной трапеции).
Следовательно, данные треугольники равны (по
второму признаку равенства треугольников).
Значит, AE=FD.
Рассмотрим треугольник ABE.
По
определению tg∠BAE=BE/AE
tg45°=5/AE=1 (по
таблице)
AE=5
EF=BC=6 (так как BCFE -
прямоугольник)
AD=AE+EF+FD=5+6+5=16
Ответ: AD=16
Поделитесь решением
Присоединяйтесь к нам...
Укажите номера верных утверждений.
1) В тупоугольном треугольнике все углы тупые.
2) В любом параллелограмме диагонали точкой пересечения делятся пополам.
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
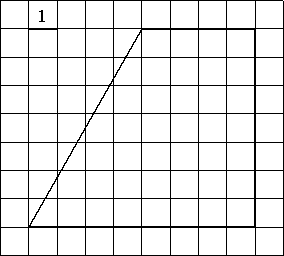Найдите площадь трапеции, изображённой на рисунке.
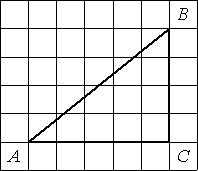Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
Основание AC равнобедренного треугольника ABC равно 8. Окружность радиуса 5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
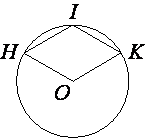Точка O – центр окружности, на которой лежат точки H, I и K таким образом, что OHIK – ромб. Найдите угол OHI. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: