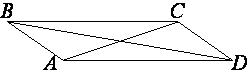
В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=169°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
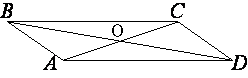Обозначим точку пересечения диагоналей как О.
По
свойству
параллелограмма AO=OC=AC/2.
AB=CD (по
другому свойству).
А так как AC в 2 раза больше стороны AB (по условию задачи), то OC=AB=CD.
Следовательно треугольник OCD -
равнобедренный.
По
свойству равнобедренного треугольника ∠COD=∠CDO.
По
теореме о сумме углов треугольника: 180°=∠COD+∠CDO+∠ACD=∠COD+∠CDO+169°
∠COD+∠CDO=11°, а так как ∠COD=∠CDO (это мы выяснили ранее), то ∠COD=∠CDO=11°/2=5,5°
∠COD - острый угол между диагоналями.
Следовательно,
∠COB=180°-∠COD=180°-5,5°=174,5° (т.к. это
смежные углы) - тупой угол между диагоналями.
Ответ: острый угол между диагоналями параллелограмма (∠COD) равен 5,5°, тупой угол между диагоналями равен 174,5°
Поделитесь решением
Присоединяйтесь к нам...
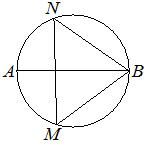На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=36°. Найдите угол NMB. Ответ дайте в градусах.
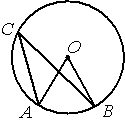Точка О – центр окружности, /ACB=32° (см. рисунок). Найдите величину угла AOB (в градусах).
В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ=44, SQ=22.
В прямоугольном треугольнике катет и гипотенуза равны 16 и 20 соответственно. Найдите другой катет этого треугольника.
В треугольнике ABC на его медиане BM отмечена точка K так, что BK:KM=10:9. Прямая AK пересекает сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: