
 Площадь параллелограмма ABCD равна 28. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
Площадь параллелограмма ABCD равна 28. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
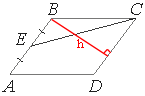 Проведем высоту
параллелограмма из угла ABC.
Проведем высоту
параллелограмма из угла ABC.
По первой формуле, площадь параллелограмма равна:
Sп=CD*h=28
h=28/CD
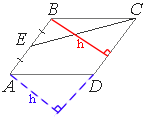 Высота параллелограмма является так же и высотой
трапеции, так как основания
трапеции и
параллелограмма лежат на одних и тех же прямых (AB и DC).
Высота параллелограмма является так же и высотой
трапеции, так как основания
трапеции и
параллелограмма лежат на одних и тех же прямых (AB и DC).
Площадь трапеции:
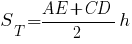
AE=AB/2 (по условию задачи).
AE=AB/2=CD/2 (по первому свойству параллелограмма).
Подставляем все полученные значения:
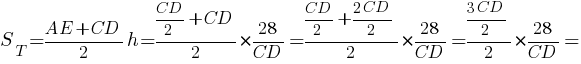
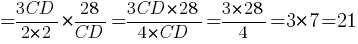
Ответ: 21
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC проведена биссектриса AL, угол ALC равен 52°, угол ABC равен 13°. Найдите угол ACB. Ответ дайте в градусах.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 52°, угол ABC равен 13°. Найдите угол ACB. Ответ дайте в градусах.
 Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=8, BF=15.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=8, BF=15.
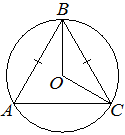 Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=57°. Найдите величину угла BOC. Ответ дайте в градусах.
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=57°. Найдите величину угла BOC. Ответ дайте в градусах.
 В трапеции ABCD AB=CD, ∠BDA=35° и ∠BDC=58°. Найдите угол ABD. Ответ дайте в градусах.
В трапеции ABCD AB=CD, ∠BDA=35° и ∠BDC=58°. Найдите угол ABD. Ответ дайте в градусах.
Укажите номера верных утверждений.
1) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.
2) Смежные углы равны.
3) Медиана равнобедренного треугольника, проведённая к его основанию, является его высотой.
Комментарии: