Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AB и CD четырёхугольника пересекаются в точке M. Докажите, что треугольники MBC и MDA подобны.
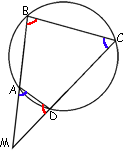Чтобы четырехугольник можно было вписать в окружность, должно выполняться условие:
∠DAB+∠BCD=∠ABC+∠CDA=180° (по третьему свойству описанной окружности
).
∠ADM является
смежным по отношению к ∠CDA, следовательно:
180°=∠ADM+∠CDA
180°=∠ABC+∠CDA (это мы установили ранее).
Получается, что ∠ADM=∠ABC
∠DAM является
смежным по отношению к ∠DAB, следовательно:
180°=∠DAM+∠DAB
180°=∠BCD+∠DAB (это мы установили ранее).
Получается, что ∠DAM=∠BCD
∠M - общий для треугольников MBC и MDA.
Тогда, по
первому признаку подобия, данные треугольники
подобны.
Поделитесь решением
Присоединяйтесь к нам...
Площадь равнобедренного треугольника равна 196√
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 1 м, а длинное плечо — 3 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
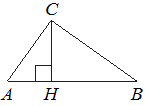На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=2, BH=18. Найдите CH.
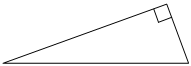В прямоугольном треугольнике катет и гипотенуза равны 7 и 25 соответственно. Найдите другой катет этого треугольника.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2019-05-19 13:34:45) Администратор: Spektra542, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и мы ее обязательно добавим.
(2019-05-14 13:05:07) Spektra542: известно что около четырёхугольника ABCD можно описать окружность и что продолжения сторон пересекаются в точке K. Докажите что углы BAD и KCD равны