
 –ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į
–ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į–ó–į–ī–į—á–į ‚ĄĖ237 –ł–∑ 1087 |
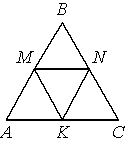 –í —Ä–į–≤–Ĺ–ĺ—Ā—ā–ĺ—Ä–ĺ–Ĺ–Ĺ–Ķ–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC —ā–ĺ—á–ļ–ł M, N, K ‚ÄĒ —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ—č —Ā—ā–ĺ—Ä–ĺ–Ĺ –ź–í, –í–°, –°–ź —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –Ē–ĺ–ļ–į–∂–ł—ā–Ķ, —á—ā–ĺ –źMNK ‚ÄĒ —Ä–ĺ–ľ–Ī.
–í —Ä–į–≤–Ĺ–ĺ—Ā—ā–ĺ—Ä–ĺ–Ĺ–Ĺ–Ķ–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC —ā–ĺ—á–ļ–ł M, N, K ‚ÄĒ —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ—č —Ā—ā–ĺ—Ä–ĺ–Ĺ –ź–í, –í–°, –°–ź —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –Ē–ĺ–ļ–į–∂–ł—ā–Ķ, —á—ā–ĺ –źMNK ‚ÄĒ —Ä–ĺ–ľ–Ī.
–ü–ĺ —É—Ā–Ľ–ĺ–≤–ł—é –∑–į–ī–į—á–ł AB=BC=CA (—ā.–ļ. —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ ABC -
—Ä–į–≤–Ĺ–ĺ—Ā—ā–ĺ—Ä–ĺ–Ĺ–Ĺ–ł–Ļ). –ó–Ĺ–į—á–ł—ā AK=KC=CN=NB=BM=MA.
–Ę–ĺ–≥–ī–į, MN -
—Ā—Ä–Ķ–ī–Ĺ—Ź—Ź –Ľ–ł–Ĺ–ł—Ź —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC. –°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, MN=AK –ł MN||AK (–Ņ–ĺ
—ā–Ķ–ĺ—Ä–Ķ–ľ–Ķ –ĺ —Ā—Ä–Ķ–ī–Ĺ–Ķ–Ļ –Ľ–ł–Ĺ–ł–ł).
NK - —ā–ĺ–∂–Ķ
—Ā—Ä–Ķ–ī–Ĺ—Ź—Ź –Ľ–ł–Ĺ–ł—Ź, —Ä–į–≤–Ĺ–į AM –ł –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ–į AM.
–ü–ĺ–Ľ—É—á–į–Ķ—ā—Ā—Ź, —á—ā–ĺ AM=MN=NK=KA, —ā.–Ķ. AMNK -
—Ä–ĺ–ľ–Ī (–Ņ–ĺ
—Ā–≤–ĺ–Ļ—Ā—ā–≤—É —Ä–ĺ–ľ–Ī–į).
–ü–ĺ–ī–Ķ–Ľ–ł—ā–Ķ—Ā—Ć —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ–ľ
–ü—Ä–ł—Ā–ĺ–Ķ–ī–ł–Ĺ—Ź–Ļ—ā–Ķ—Ā—Ć –ļ –Ĺ–į–ľ...
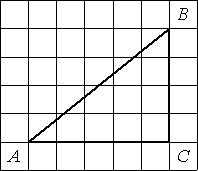 –Ě–į–Ļ–ī–ł—ā–Ķ —ā–į–Ĺ–≥–Ķ–Ĺ—Ā —É–≥–Ľ–į –ź —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC, –ł–∑–ĺ–Ī—Ä–į–∂—Ď–Ĺ–Ĺ–ĺ–≥–ĺ –Ĺ–į —Ä–ł—Ā—É–Ĺ–ļ–Ķ.
–Ě–į–Ļ–ī–ł—ā–Ķ —ā–į–Ĺ–≥–Ķ–Ĺ—Ā —É–≥–Ľ–į –ź —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC, –ł–∑–ĺ–Ī—Ä–į–∂—Ď–Ĺ–Ĺ–ĺ–≥–ĺ –Ĺ–į —Ä–ł—Ā—É–Ĺ–ļ–Ķ.
–ö–ĺ—Ā–ł–Ĺ—É—Ā –ĺ—Ā—ā—Ä–ĺ–≥–ĺ —É–≥–Ľ–į A —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC —Ä–į–≤–Ķ–Ĺ 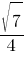 . –Ě–į–Ļ–ī–ł—ā–Ķ sinA.
. –Ě–į–Ļ–ī–ł—ā–Ķ sinA.
 –ü–Ľ–ĺ—Č–į–ī—Ć –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ä–į–≤–Ĺ–į 578√
–ü–Ľ–ĺ—Č–į–ī—Ć –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ä–į–≤–Ĺ–į 578√
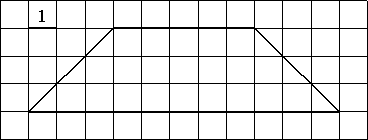 –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —ā—Ä–į–Ņ–Ķ—Ü–ł–ł, –ł–∑–ĺ–Ī—Ä–į–∂—Ď–Ĺ–Ĺ–ĺ–Ļ –Ĺ–į —Ä–ł—Ā—É–Ĺ–ļ–Ķ.
–Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —ā—Ä–į–Ņ–Ķ—Ü–ł–ł, –ł–∑–ĺ–Ī—Ä–į–∂—Ď–Ĺ–Ĺ–ĺ–Ļ –Ĺ–į —Ä–ł—Ā—É–Ĺ–ļ–Ķ.
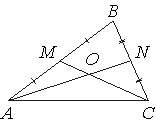 –Ę–ĺ—á–ļ–ł M –ł N —Ź–≤–Ľ—Ź—é—ā—Ā—Ź —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ–į–ľ–ł —Ā—ā–ĺ—Ä–ĺ–Ĺ AB –ł BC —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –ě—ā—Ä–Ķ–∑–ļ–ł AN
–ł CM –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—ā—Ā—Ź –≤ —ā–ĺ—á–ļ–Ķ O, AN=21, CM=15. –Ě–į–Ļ–ī–ł—ā–Ķ OM.
–Ę–ĺ—á–ļ–ł M –ł N —Ź–≤–Ľ—Ź—é—ā—Ā—Ź —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ–į–ľ–ł —Ā—ā–ĺ—Ä–ĺ–Ĺ AB –ł BC —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –ě—ā—Ä–Ķ–∑–ļ–ł AN
–ł CM –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—ā—Ā—Ź –≤ —ā–ĺ—á–ļ–Ķ O, AN=21, CM=15. –Ě–į–Ļ–ī–ł—ā–Ķ OM.
–ö–ĺ–ľ–ľ–Ķ–Ĺ—ā–į—Ä–ł–ł: