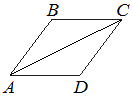
В ромбе ABCD угол ABC равен 146°. Найдите угол ACD. Ответ дайте в градусах.
Рассмотрим треугольник ABC.
AB=BC (по определению ромба).
Следовательно, треугольник ABC -
равнобедренный.
∠CAB=∠ACB (по свойству равнобедренного треугольника).
По
теореме о сумме углов треугольника:
180°=∠CAB+∠ACB+∠ABC
180°=∠ACB+∠ACB+146°
180°-146°=2*∠ACB
34°=2*∠ACB
∠ACB=17°
Рассмотрим треугольники ABC и ADC:
1) AB=BC=CD=DA (по определению ромба).
2) AC - общая сторона.
Тогда по 3-му признаку данные треугольники равны.
Следовательно:
∠ACD=∠ACB=17°
Ответ: 17
Поделитесь решением
Присоединяйтесь к нам...
Радиус окружности, описанной около квадрата, равен 14√
Синус острого угла A треугольника ABC равен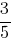 
. Найдите CosA.
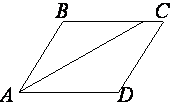Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 14°. Ответ дайте в градусах.
В трапецию, сумма длин боковых сторон которой равна 18, вписана окружность. Найдите длину средней линии трапеции.
Сторона AB параллелограмма ABCD вдвое больше стороны AD. Точка K — середина стороны AB. Докажите, что DK — биссектриса угла ADC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: