Радиус окружности, описанной около квадрата, равен 36√2. Найдите длину стороны этого квадрата.
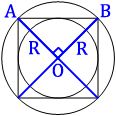Проведем диаметры
описанной окружности, как показано на первом рисунке.
Очевидно, что
квадрат разделился на 4 равных треугольника, углы, которые опираются на центр окружности (О), равны 360°/4=90°, т.е. эти треугольники
прямоугольные.
Тогда, по теореме Пифагора:
AB2=R2+R2
AB2=2R2
AB2=2(36√
AB2=2*362*2
AB2=362*22=(36*2)2=722
AB=72
Ответ: 72
Поделитесь решением
Присоединяйтесь к нам...
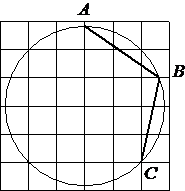Найдите угол ABC . Ответ дайте в градусах.
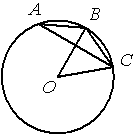Точка О – центр окружности, /BOC=50° (см. рисунок). Найдите величину угла BAC (в градусах).
Радиус окружности, описанной около квадрата, равен 14√
В трапеции ABCD AB=CD, ∠BDA=35° и ∠BDC=58°. Найдите угол ABD. Ответ дайте в градусах.
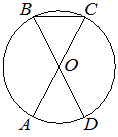В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 50°. Найдите угол ACB. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: