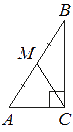
В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=60, BC=40. Найдите CM.
Так как треугольник ABC прямоугольный, то воспользуемся теоремой об описанной окружности для прямоугольного треугольника. Для этого опишем окружность вокруг треугольника ABC.
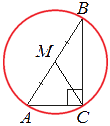Центр описанной вокруг прямоугольного треугольника окружности лежит на середине гипотенузы.
Получается, что точка М и есть центр окружности, следовательно:
R=AM=MB=AB/2=60/2=30
CM тоже является радиусом окружности, т.е.:
CM=R=30
Ответ: 30
Поделитесь решением
Присоединяйтесь к нам...
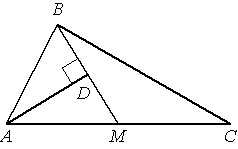Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АВ, если сторона АС равна 10.
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 62°. Найдите величину угла OMK. Ответ дайте в градусах.
Точка О – центр окружности, /ACB=24° (см. рисунок). Найдите величину угла AOB (в градусах).
Один из острых углов прямоугольного треугольника равен 57°. Найдите его другой острый угол. Ответ дайте в градусах.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=1:2, KM=23.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: