Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=5, а расстояние от точки K до стороны AB равно 5.
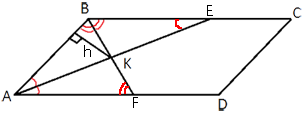Обозначим точки пересечения
биссектрис со сторонами как показано на рисунке.
∠FAK=∠BEK (т.к. это
накрест-лежащие углы).
Получается, что ∠BAK=∠BEK, следовательно треугольник ABE -
равнобедренный (по
свойству равнобедренного треугольника).
Тогда AB=BE.
Треугольники ABK и EBK равны по
первому признаку равенства треугольников.
Следовательно и
высоты у этих треугольников тоже равны.
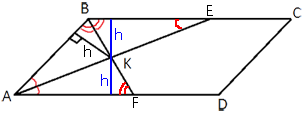Аналогично, равны и треугольники ABK и AFK.
Получается, что высота
параллелограмма равна 2h.
Площадь
параллелограмма равна SABCD=2h*BC=2*5*5=50
Ответ: 50
Поделитесь решением
Присоединяйтесь к нам...
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника COD.
Укажите номера верных утверждений.
1) Любой квадрат является ромбом.
2) Против равных сторон треугольника лежат равные углы.
3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
Основание AC равнобедренного треугольника ABC равно 16. Окружность радиуса 12 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
В треугольнике два угла равны 46° и 78°. Найдите его третий угол. Ответ дайте в градусах.
В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=48 и CH=2. Найдите cosB.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-10-07 22:45:45) Администратор: Валерий, спасибо за подсказку другого подхода к решению.
(2015-10-07 22:28:15) Валерий: Точки, лежащие на биссектрисах углов равноудалены от сторон этих углов, значит точка К равноудалена от AB, AD и BC, тогда расстояние от точки К до ВС равно расстоянию от точки К до AD и равно расстоянию от точки К до АВ, т.е. равно 5. Тогда высота H к ВС равна 10 и SABCD=H*BC=10*5=50. Ответ: 50. Благодарю авторов за сайт и за ответ.