
 Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 57.
Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 57.
 Для удобства введем обозначения:
Для удобства введем обозначения:
a - сторона
ромба (они равны по
определению ромба)
d - диагональ AC
57d - диагональ BD (по условию)
AE - k
EB - t
Площадь
параллелограмма через диагонали равна BD*AC*sinα/2 = 57d*d*sinα/2 = 28,5d2*sinα, где α - угол между диагоналями (при чем не важно какой, так как синусы обоих углов будут равны друг другу).
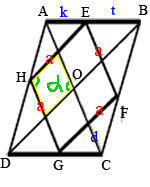 Так как стороны
ромба параллельны диагоналям, образуется маленький
параллелограмм, а значит противоположные углы равны (по
свойству параллелограмма).
Так как стороны
ромба параллельны диагоналям, образуется маленький
параллелограмм, а значит противоположные углы равны (по
свойству параллелограмма).
Рассмотрим треугольники ABC и EBF.
∠EBF - общий
∠BFE=∠BCA (это
соответственные углы)
Следовательно, треугольники ABC и EBF
подобны (по
первому признаку подобия).
Тогда EF/AC=a/d=t/(t+k)
Аналогично,
подобны и треугольники ABD и AEH.
Для них справедливо: a/57d=k/(t+k)
Складываем эти два уравнения:
a/d+a/57d=t/(t+k)+k/(t+k)
57a/57d+a/57d=(t+k)/(t+k)
58a/57d=1
58a=57d
a=57d/58
Sромба=a2sinα
Sпараллелограмма=28,5d2*sinα (это мы выяснили ранее)
Sромба/Sпараллелограмма=(a2sinα)/(28,5d2*sinα)=a2/(28,5d2)=(57d/58)2/(28,5d2)=(572*d2)/(582*28,5*d2)=3249/(3364*28,5)=114/3364=57/1682
Ответ: 57/1682
Поделитесь решением
Присоединяйтесь к нам...
 Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 39°. Найдите величину угла OMK. Ответ дайте в градусах.
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 39°. Найдите величину угла OMK. Ответ дайте в градусах.
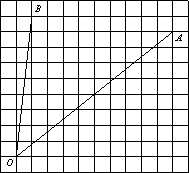 Найдите тангенс угла
AOB.
Найдите тангенс угла
AOB.
 На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что /NBA=38°. Найдите угол NMB. Ответ дайте в градусах.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что /NBA=38°. Найдите угол NMB. Ответ дайте в градусах.
 В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 1. Найдите площадь трапеции.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 1. Найдите площадь трапеции.
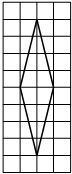 На клетчатой бумаге с размером клетки 1x1 изображён ромб. Найдите площадь этого ромба.
На клетчатой бумаге с размером клетки 1x1 изображён ромб. Найдите площадь этого ромба.

Комментарии: