Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите AB, если BC=40.
BC||AD (по
определению параллелограмма)
∠BAE=∠EAD (т.к. AE -
биссектриса)
∠EAD=∠BEA (т.к. это
накрест-лежащие углы)
Следовательно, ∠BAE=∠BEA
Получается, что треугольник ABE -
равнобедренный (по
свойству), и AB=BE (по
определению равнобедренного треугольника).
Аналогично с треугольником ECD:
∠CED=∠CDE
EC=CD
Так как AB=CD (по
свойству параллелограмма), то получается, что AB=BE=EC=CD.
Значит, BE=BC/2=40/2=20.
AB=BE=20
Ответ: AB=20
Поделитесь решением
Присоединяйтесь к нам...
На отрезке AB выбрана точка C так, что AC=60 и BC=27. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 55°. Найдите величину угла ODC.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 164. Найдите стороны треугольника ABC.
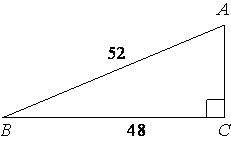Найдите площадь треугольника, изображённого на рисунке.
Площадь параллелограмма равна 60, а две его стороны равны 4 и 20. Найдите его высоты. В ответе укажите большую высоту.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-03-21 21:56:44) Мария: Огромное спасибо, ваш сайт мне очень помогает для подготовки к ОГЭ