Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=63. Диагональ параллелограмма BD равна 65. Найдите площадь параллелограмма.
Рассмотрим треугольник BDH.
Данный треугольник
прямоугольный, следовательно можно применить
теорему Пифагора:
BD2=HD2+BH2
652=632+BH2
4225=3969+BH2
BH2=256
BH=16
Найдем площадь
параллелограмма:
S=AD*BH=(AH+HD)*BH=(1+63)*16=1024
Ответ: 1024
Поделитесь решением
Присоединяйтесь к нам...
Найдите площадь квадрата, описанного около окружности радиуса 32.
В равнобедренную трапецию, периметр которой равен 180, а площадь равна 1620, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=13.
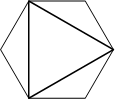Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.
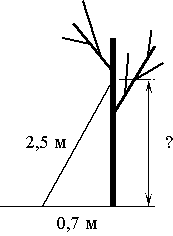Лестницу длиной 2,5 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 0,7 м?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-02-20 20:22:44) Администратор: Сумая, в чем вопрос.
(2017-02-20 18:12:06) Сумая: Сумма треугольников