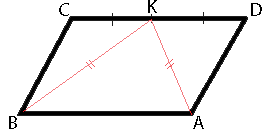
В параллелограмме ABCD точка K — середина стороны CD. Известно, что KA=KB. Докажите, что данный параллелограмм — прямоугольник.
Рассмотрим треугольники BCK и KDA. CK=KD, т.к. точка K - середина CD, KA=KB (из условия задачи), CB=AD (по свойству параллелограмма). Соответственно, треугольники BCK и KDA равны (по третьему признаку равенства треугольников).
Из равенства этих треугольников следует, что /BCK=/KDA.
BC||AD (по определению параллелограмма), рассмотрим сторону CD как секущую к этим параллельным сторонам. Тогда получается, что сумма углов BCK и KDA равна 180°, т.к. эти углы являются внутренними односторонними. Отсюда следует, что каждый из этих углов равен 90°.
Теперь рассмотрим стороны AB и CD, они параллельны (тоже по определению параллелограмма). Рассмотрим сторону BC как секущую к этим параллельным сторонам.
/CBA и /KCB - внутренние односторонние. Следовательно их сумма равна 180°. А так как /KCB=90°, то /CBA тоже равен 90°.
Аналогично доказывается, что /DAB тоже равен 90°.
Параллелограмм, у которого все углы прямые (т.е. 90°) называется прямоугольником (по определению).
Поделитесь решением
Присоединяйтесь к нам...
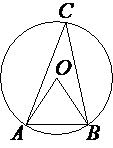Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 27°.
На окружности отмечены точки A и B так, что меньшая дуга AB равна 92°. Прямая BC касается окружности
в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
На клетчатой бумаге с размером клетки 1x1 изображён параллелограмм. Найдите его площадь.
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник ACP, равен 12 см, тангенс угла ABC равен 2,4. Найдите радиус вписанной окружности треугольника ABC.
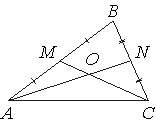Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=21, CM=15. Найдите OM.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: