Какие из данных утверждений верны? Запишите их номера.
1) У равнобедренного треугольника есть ось симметрии.
2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.
3) Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
Рассмотрим каждое утверждение.
1) "У
равнобедренного треугольника есть ось симметрии", это утверждение верно, ось совпадает с
высотой, опущенной к основанию треугольника.
2) "Если в
параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат", это утверждение верно, т.к. оно совпадает со
свойством квадрата.
3) "Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности", это утверждение неверно, окружности не будут пересекаться, если, например, центры окружностей совпадают.
Поделитесь решением
Присоединяйтесь к нам...
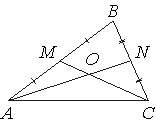Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=21, CM=15. Найдите OM.
Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK=7, CK=12.
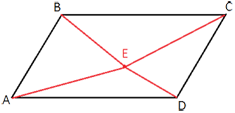Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.
Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD=10. Докажите, что треугольники CBD и ADB подобны.
В трапеции ABCD AB=CD, ∠BDA=62° и ∠BDC=42°. Найдите угол ABD. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: