В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 6. Найдите площадь трапеции.
Вариант 1 (предложил пользователь Всеволод)
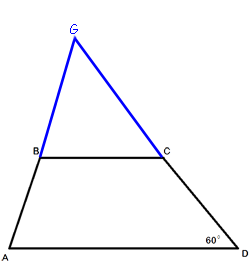Продолжим стороны AB и CD до пересечения в точке G.
BC || AD (по
определению трапеции).
AD вдвое больше BC (по условию задачи), следовательно:
BC -
средняя линия для треугольника AGD.
Тогда, CD=CG=AD/2 (по
теореме о средней линии).
Получается, что AD=DG, т.е. треугольник AGD -
равнобедренный.
Следовательно, ∠AGD=∠GAD=x (
свойство равнобедренного треугольника)
По
теореме о сумме углов треугольника:
180°=∠AGD+∠GAD+∠ADG
180°=x+x+60°
120°=2x
x=60°, т.е. все углы треугольника ADG равны 60°, следовательно данный треугольник
равносторонний.
Следовательно, AG=DG, тогда и AB=CD, т.е.
трапеция ABCD
равнобедренная.
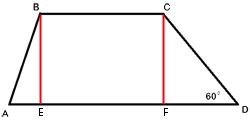Проведем
высоты BE и CF как показано на рисунке.
AD=AE+EF+FD, EF=BC=6 (так как BCFE -
прямоугольник), AE=FD=y (так как трапеция равнобедренная).
12=y+6+y
y=3
По
теореме Пифагора CD2=CF2+FD2
62=CF2+32
CF2=27, CF=3√
SABCD=((BC+AD)/2)*CF=((6+12)/2)*3√
SABCD=27√
Ответ: SABCD=27√
Проведем
высоты BE и CF как показано на рисунке.Поделитесь решением
Присоединяйтесь к нам...
В прямоугольном треугольнике ABC катет AC=35, а высота CH, опущенная на гипотенузу, равна 14√
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=20, DK=15, BC=12. Найдите AD.
На окружности отмечены точки A и B так, что меньшая дуга AB равна 66°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 4 м?
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
2) Диагональ трапеции делит её на два равных треугольника.
3) Если в ромбе один из углов равен
90°, то такой ромб — квадрат.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-03-15 18:10:35) Администратор: Всеволод, согласен с Вами!
(2015-03-15 17:49:50) Всеволод: Уважаемый Администратор! Спасибо Вам за ведение такого полезного ресурса. Спасибо и за оценку моего дополнения. На мой взгляд, чем больше разных подходов, тем шире понимание у всех интересующихся.
(2015-03-14 22:00:48) Администратор: Всеволод, очень неплохой вариант! В скором времени опубликую по Вашим именем.
(2015-03-14 18:21:37) Всеволод: Предлагаю чуть другой вариант первой половины решения. Продолжим стороны AB и CD до пересечения в точке G. Для треугольника ADG основание трапеции BC (BC=AD/2) будет средней линией, значит CD=CG=AD/2, отсюда AD=DG, а угол между ними 60 градусов, значит треугольник ADG равносторонний, а тогда трапеция равнобедренная.