В треугольнике ABC DE – средняя линия. Площадь треугольника CDE равна 35. Найдите площадь треугольника ABC.
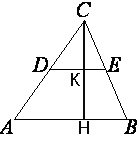Проведем
высоту CH.
Средняя линия делит CH пополам, как и стороны треугольника.
Следовательно, CK=KH.
По
теореме о средней линии AB=2DE.
SCDE=DE*CK/2=35.
DE*CK=70
SABC=AB*CH/2=2DE*2CK/2=2DE*CK=2*70=140
Ответ: SABC=140
Поделитесь решением
Присоединяйтесь к нам...
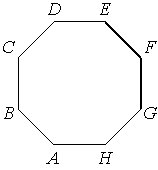ABCDEFGH – правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.
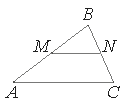Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=36, MN=28. Площадь треугольника ABC равна 162. Найдите площадь треугольника MBN.
Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
Человек, рост которого равен 1,8 м, стоит на расстоянии 16 м от уличного фонаря. При этом длина тени человека равна 9 м. Определите высоту фонаря (в метрах).
Человек ростом 1,5 м стоит на расстоянии 7 м от столба, на котором висит фонарь на высоте 3,6 м. Найдите длину тени человека в метрах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: