
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABC к площади четырёхугольника KPCM.
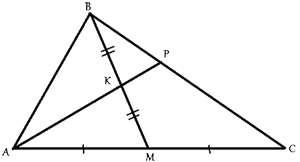 По условию задачи ВМ -
медиана треугольника АВС, следовательно, по
свойству медианы,
площади треугольников АВМ и ВСМ равны, и равны половине площади треугольника АВС.
По условию задачи ВМ -
медиана треугольника АВС, следовательно, по
свойству медианы,
площади треугольников АВМ и ВСМ равны, и равны половине площади треугольника АВС.
SABM=SBCM=(SABC)/2.
В свою очередь, AK является медианой для треугольника АВМ, следовательно, по тому же
свойству медианы
SABК=SAKM=(SABM)/2=(SABC)/4.
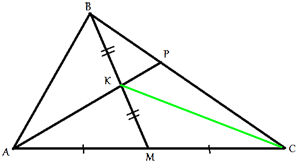 Проведем отрезок СК.
СК является
медианой для треугольника СМВ, следовательно,
Проведем отрезок СК.
СК является
медианой для треугольника СМВ, следовательно,
SCMK=SCKB=(SCMB)/2=(SABC)/4.
Проведем отрезок МЕ, параллельно АР.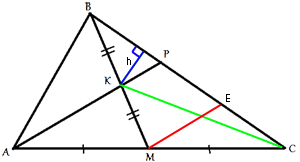 МЕ является
средней линией для треугольника АРС, следовательно (по
теореме о средней линии) СЕ=ЕР. А для треугольника МВЕ
КР является
средней линией, следовательно ВР=ЕР(=СЕ). Т.е. сторона ВС делится на три равные части точками
Р и Е.
МЕ является
средней линией для треугольника АРС, следовательно (по
теореме о средней линии) СЕ=ЕР. А для треугольника МВЕ
КР является
средней линией, следовательно ВР=ЕР(=СЕ). Т.е. сторона ВС делится на три равные части точками
Р и Е.
Проведем
высоту h, как показано на рисунке. h является общей высотой для треугольников СКВ и СКР.
Выше мы определили, что SCKB=(SABC)/4. Площадь этого же треугольника =(1/2)*h*BC.
SCKP=(1/2)*h*РС=(1/2)*h*(2/3)*ВС=(2/3)*(1/2)*h*BC=(2/3)SCKB=(2/12)SABC
=(1/6)SABC.
SKPCM=SCMK+SCKP=(SABC)/4+(1/6)SABC=(5/12)SABC.
SABC/SKPCM=12/5.
Ответ: SABC/SKPCM=12/5=2,4.
Поделитесь решением
Присоединяйтесь к нам...
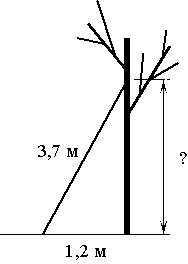 Лестницу длиной 3,7 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,2 м?
Лестницу длиной 3,7 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,2 м?
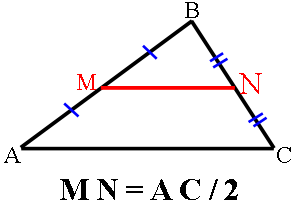
 Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
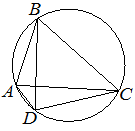 Четырёхугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах.
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах.
 Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=6, AC=24.
Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=6, AC=24.
 Две касающиеся внешним образом в точке K окружности, радиусы которых равны 45 и 46, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 45 и 46, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
Комментарии:
(2015-05-26 03:55:13) Сергей: Это задание С6, то есть 26. Было в ГИА по математике 28.05.2013.
(2015-05-24 17:25:48) Администратор: Валерия, к сожалению, у меня нет такой информации.
(2015-05-24 13:29:05) Валерия: Это задание из части С?) Просто по сложности не похоже на часть B, вот интересно это задание C4 или C6?( то есть в геометрии из части С первое задание или последнее), там вроде 24 или 26 задание, так наверное правильнее сказать
(2015-05-24 11:49:55) Администратор: Валерия, а что такое c4 и c6?
(2015-05-24 11:31:16) Валерия: Это c4 или c6?