
 Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=24, CM=15. Найдите AO.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=24, CM=15. Найдите AO.
Отрезки AN и CM - являются
медианами треугольника ABC.
Тогда, применяя первое свойство медианы, можем записать:
AO/ON=2/1, т.е. ON=AO/2
При этом AN=AO+ON
24=AO+ON, подставляем в это уравнение первое равенство:
24=AO+AO/2 |*2
48=2AO+AO
48=3AO
AO=16
Ответ: 16
Поделитесь решением
Присоединяйтесь к нам...
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Найдите длину стороны AC, если радиус описанной окружности треугольника ABC равен 7.
 В треугольнике ABC известно, что AB=BC, ∠ABC=122°. Найдите угол BCA. Ответ дайте в градусах.
В треугольнике ABC известно, что AB=BC, ∠ABC=122°. Найдите угол BCA. Ответ дайте в градусах.
Какое из следующих утверждений верно?
1) Площадь квадрата равна произведению двух его смежных сторон.
2) Диагональ трапеции делит её на два равных треугольника.
3) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
 В трапеции ABCD AB=CD, AC=AD и ∠ABC=123°. Найдите угол CAD. Ответ дайте в градусах.
В трапеции ABCD AB=CD, AC=AD и ∠ABC=123°. Найдите угол CAD. Ответ дайте в градусах.
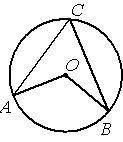 Точка О – центр окружности, /ACB=70° (см. рисунок). Найдите величину угла AOB (в градусах).
Точка О – центр окружности, /ACB=70° (см. рисунок). Найдите величину угла AOB (в градусах).
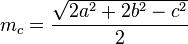 , где mc — медиана к стороне c; a, b, c — стороны треугольника. В частности, сумма квадратов медиан произвольного треугольника в 4/3 раза меньше суммы квадратов его сторон:
, где mc — медиана к стороне c; a, b, c — стороны треугольника. В частности, сумма квадратов медиан произвольного треугольника в 4/3 раза меньше суммы квадратов его сторон: 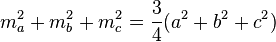
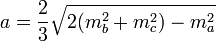 , где ma, mb, mc медианы к соответствующим сторонам треугольника, a, b, c — стороны треугольника.
, где ma, mb, mc медианы к соответствующим сторонам треугольника, a, b, c — стороны треугольника.
Комментарии: