Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 48, а площадь равна 288.
Решение прислал пользователь Людмила
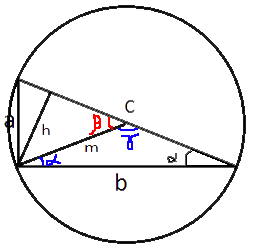Проведем из прямого угла медиану и высоту, обозначив их m и h соответственно.
Если описать окружность вокруг треугольника, то центр этой окружности будет лежать на середине гипотенузы (по
теореме об описанной окружности). Следовательно:
m=c/2=48/2=24
S=(1/2)hc
h=2S/c=2*288/48=288/24=12
По
определению синуса:
sinβ=h/m=12/24=0,5
По таблице определяем, что β=30°
Угол γ является внешнем к β, следовательно γ=180°-β=180°-30°=150°
Треугольник, содержащий угол γ,
равнобедренный, так как медиана m и половина гипотенузы равны (это мы выяснили ранее).
Следовательно, по
свойству равнобедренного треугольника углы при основании равны (обозначены α).
Тогда, по
теореме о сумме углов треугольника:
180°=γ+α+α
180°=150°+2α
α=15° - это один из искомых углов.
Другой искомый угол найдем по той же
теореме об углах треугольника: 180°-90°-15°=75°
ответ: 15° и 75°
Поделитесь решением
Присоединяйтесь к нам...
Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 1,8 м, высота большой опоры 2,8 м. Найдите высоту средней опоры.
В треугольнике ABC угол C равен 90°, AC=10, tgA=0,1. Найдите BC.
Найдите площадь треугольника, изображённого на рисунке.
Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит больший угол.
2) Любой прямоугольник можно вписать в окружность.
3) Площадь треугольника меньше произведения двух его сторон.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 15. Найдите BC, если AC=24.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: