Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠C, если ∠A=81°. Ответ дайте в градусах.
Так как сторона AC треугольника ABC проходит через центр
описанной около него окружности, то AC - это диаметр окружности.
Следовательно, треугольник ABC - прямоугольный (по
свойству описанной окружности), т.е. ∠B=90°.
По
теореме о сумме углов треугольника:
∠A+∠B+∠C=180°
81°+90°+∠C=180°
∠C=180°-81°-90°
∠C=9°
Ответ: 9
Поделитесь решением
Присоединяйтесь к нам...
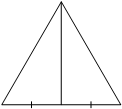Радиус окружности, вписанной в равносторонний треугольник, равен 10√3. Найдите длину стороны этого треугольника.
В треугольнике ABC угол C равен 90°, AC=6, AB=10. Найдите sinB.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
25° и 110°. Найдите меньший угол параллелограмма.
Площадь равнобедренного треугольника равна 144√
Укажите номера верных утверждений.
1) Существует квадрат, который не является прямоугольником.
2) Если два угла треугольника равны, то равны и противолежащие им стороны.
3) Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: