Углы при одном из оснований трапеции равны 48° и 42°, а отрезки, соединяющие середины противоположных сторон трапеции равны 6 и 3. Найдите основания трапеции.
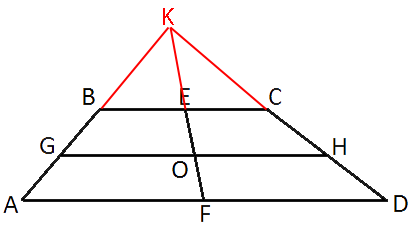Продлим стороны AB и CD до пересечения в точке K.
Рассмотрим треугольник AKD.
По
теореме о сумме углов треугольника:
∠AKD+∠KDA+∠DAK=180°
∠AKD+48°+42°=180°
∠AKD=90°
Следовательно треугольник AKD -
прямоугольный с гипотенузой AD.
KF -
медиана (по условию задачи).
Мысленно опишем вокруг этого треугольника окружность. Так как треугольник
прямоугольный, то центр окружности располагается на середине гипотенузы AD (по
теореме об описанной окружности).
Следовательно AF=FD=R - радиус окружности,
медиана KF тоже равна радиусу и, следовательно, равна AD/2.
Рассмотрим треугольник GKH.
Для этого треугольника KO -
медиана и равна половине гипотенузы GH (как и у предыдущего треугольника).
KO=OH=GH/2
В треугольнике BKC - аналогичная ситуация: KE=EC=BC/2
Вернемся к треугольнику GKH:
KO=OH=GH/2=6/2=3
3=OH=KE+EO=EC+EF/2
EC=3-EF/2=3-3/2=1,5
BC=2*EC=2*1,5=3
Рассмотрим трапецию ABCD.
GH -
средняя линия, следовательно GH=(BC+AD)/2
2GH=BC+AD
AD=2GH-BC=2*6-3=12-3=9
Ответ: AD=9, BC=3
Поделитесь решением
Присоединяйтесь к нам...
Прямая касается окружности в точке K. Центр окружности – точка O. Хорда KM образует с касательной угол, равный 40°. Найдите величину угла KOM. Ответ дайте в градусах.
На окружности отмечены точки A и B так, что меньшая дуга AB равна 66°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
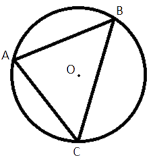Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:4:11. Найдите радиус окружности, если меньшая из сторон равна 14.
Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=8, CK=13.
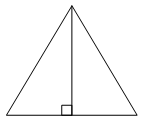Высота равностороннего треугольника равна 15√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2014-05-26 13:09:19) : вы сами все решаете?))