Радиус окружности, вписанной в трапецию, равен 24. Найдите высоту этой трапеции.
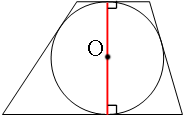Проведем радиусы к точкам касания с основаниями трапеции.
По первому свойству касательной (основания трапеции), она перпендикулярна радиусу.
Так как радиусы одновременно перпендикулярны параллельным основаниям трапеции, то получается, что радиусы представляют из себя единый отрезок или диаметр (это можно доказать если рассмотреть углы при параллельных прямых и секущей. Прямые углы являются односторонними и их сумма равна 180°).
Диаметр и является высотой трапеции:
h=D=2*R=2*24=48
Ответ: 48
Поделитесь решением
Присоединяйтесь к нам...
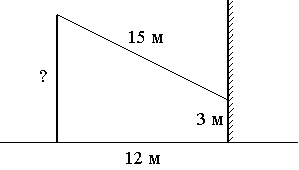От столба к дому натянут провод длиной 15 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 12 м.
Укажите номера верных утверждений.
1) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.
2) Смежные углы равны.
3) Медиана равнобедренного треугольника, проведённая к его основанию, является его высотой.
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Найдите длину стороны AC, если радиус описанной окружности треугольника ABC равен 7.
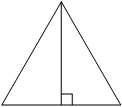Высота равностороннего треугольника равна 13√3. Найдите сторону этого треугольника.
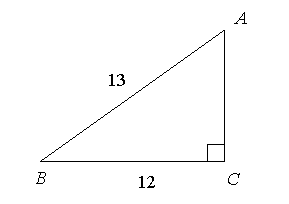Найдите площадь треугольника, изображённого на рисунке.
Хочу получать новые решения
Ни какого спама
, или 
, где m - средняя линия трапеции. 
Автор: Таська
Комментарии: