
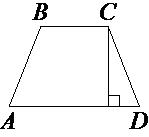 Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 1 и 5. Найдите длину основания BC.
Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 1 и 5. Найдите длину основания BC.
 Проведем отрезок из точки B перпендикулярно AD, как показано на рисунке.
Проведем отрезок из точки B перпендикулярно AD, как показано на рисунке.
BCEF - прямоугольник.
Рассмотрим треугольники ABF и DCE.
∠BAF=∠CDE (по второму свойству равнобедренной трапеции).
∠BFA=∠CED=90°
Следовательно, ∠ABF=∠DCE (по теореме о сумме углов треугольника).
AB=CD (по определению равнобедренной трапеции).
Тогда, по второму признаку данные треугольники равны.
Следовательно AF=DE=1.
FE=AE-DE=5-1=4
BC=FE=4 (по свойству прямоугольника).
Ответ: 4
Поделитесь решением
Присоединяйтесь к нам...
 Найдите площадь трапеции, диагонали которой равны 15 и 7, а средняя линия равна 10.
Найдите площадь трапеции, диагонали которой равны 15 и 7, а средняя линия равна 10.
 Лестница соединяет точки A и B. Высота каждой ступени равна 13 см, а длина – 84 см. Расстояние между точками A и B составляет 25,5 м. Найдите высоту, на которую поднимается лестница (в метрах).
Лестница соединяет точки A и B. Высота каждой ступени равна 13 см, а длина – 84 см. Расстояние между точками A и B составляет 25,5 м. Найдите высоту, на которую поднимается лестница (в метрах).
 В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=88 и BC=BM. Найдите AH.
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=88 и BC=BM. Найдите AH.
 Центральный угол AOB опирается на хорду АВ длиной 6. При этом угол ОАВ равен 60°. Найдите радиус окружности.
Центральный угол AOB опирается на хорду АВ длиной 6. При этом угол ОАВ равен 60°. Найдите радиус окружности.
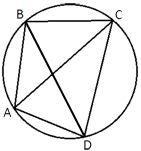 Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.
Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.

 , или
, или  , где m - средняя линия трапеции.
, где m - средняя линия трапеции.
Комментарии: