Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 135°, а CD=36.
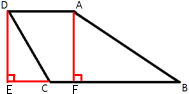Дочертим отрезки как показано на рисунке.
DE=AF, т.к. это
высоты
трапеции.
∠DCE=180°-∠BCD=180°-135°=45° (т.к. это
смежные углы).
sin(∠DCE)=ED/CD (по
определению)
sin45°=ED/CD (sin45°=√
√
ED=36√
sin(∠ABF)=AF/AB (по
определению)
sin60°=ED/AB
AB=ED/sin60° (sin60°=√
AB=(18√
Ответ: AB=12√
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике со сторонами 15 и 3 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
Сторона ромба равна 24, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
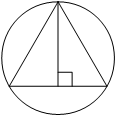Радиус окружности, описанной около равностороннего треугольника, равен 6. Найдите высоту этого треугольника.
Сторона ромба равна 20, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
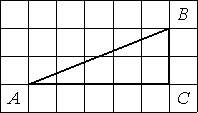Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Хочу получать новые решения
Ни какого спама
, или 
, где m - средняя линия трапеции. 
Автор: Таська
Комментарии: