Основания трапеции относятся как 2:3. Через точку пересечения диагоналей проведена прямая, параллельная основаниям. В каком отношении эта прямая делит площадь трапеции?
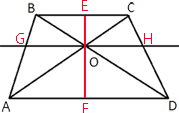По девятому свойству трапеции треугольники AOD и BOC -
подобны.
Следовательно, BC/AD=OC/AO=2/3
Проведем через точку пересечения диагоналей отрезок, перпендикулярный основаниям.
Рассмотрим треугольники AOF и COE.
∠OAF=∠OCE (
накрест-лежащие углы).
∠AFO=∠CEO=90°
Следовательно, данные треугольники
подобны (по
первому признаку подобия треугольников).
Тогда, OC/AO=OE/OF=2/3
Для простоты обозначим BC как 2x, а AD как 3x
По
пятому свойству
трапеции GH=2*2x*3x/(2x+3x)=12x2/5x=12x/5
Площадь верхней
трапеции:
S1=(BC+GH)*EO/2=(2x+12x/5)*EO/2=(10x+12x)*EO/10=22x*EO/10
Площадь нижней
трапеции:
S2=(AD+GH)*OF/2=(3x+12x/5)*OF/2=(15x+12x)*OF/10=27x*OF/10
S1/S2=(22x*EO/10)/(27x*OF/10)=(22x*EO)/(27x*OF)=22EO/27OF=22*2/(27*3)=44/81
Ответ: 44/81
Поделитесь решением
Присоединяйтесь к нам...
Лестница соединяет точки A и B. Высота каждой ступени равна 10,5 см, а длина – 36 см. Расстояние между точками A и B составляет 15 м. Найдите высоту, на которую поднимается лестница (в метрах).
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AK=18, а сторона AC в 1,2 раза больше стороны BC.
Прямые m и n параллельны. Найдите ∠3, если ∠1=6°, ∠2=101°. Ответ дайте в градусах.
Сторона AC треугольника ABC проходит через центр окружности. Найдите ∠C, если ∠A=30°. Ответ дайте в градусах.
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 4 м?
Хочу получать новые решения
Ни какого спама
, или 
, где m - средняя линия трапеции. 
Автор: Таська
Комментарии:
(2019-04-29 00:31:44) Администратор: Наталья, нажимайте на ссылки в решении задачи, откроется окно с пояснениями.
(2019-04-29 00:20:55) наталья: что это за пятое свойство трапеции?