ABCDEFGHIJ – правильный десятиугольник. Найдите угол IBJ. Ответ дайте в градусах.
Вариант 1 (Предложил пользователь Светлана)
Вокруг любого
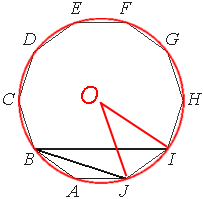
правильного многоугольника можно описать окружность, сделаем это.
Очевидно, что отрезки, проведенные из центра окружности к углам десятиугольника образуют равные углы, так как разбивают десятиугольник на равные треугольники.
Такой угол (например ∠IOJ) равен 360°/10=36°
∠IOJ является
центральным, следовательно градусная мера дуги тоже равна 36°
∠IBJ тоже опирается на эту же дугу, но является
вписанным, следовательно:
∠IBJ=36°/2=18° (по
теореме о вписанном угле)
Ответ: 18
Поделитесь решением
Присоединяйтесь к нам...
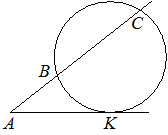Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=8, BC=24. Найдите AK.
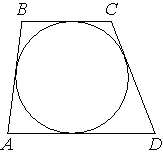Трапеция ABCD с основаниями AD и BC описана около окружности, AB=14, BC=8, CD=12. Найдите AD.
Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=5, CK=14.
Сторона квадрата равна 4√2. Найдите радиус окружности, описанной около этого квадрата.
Укажите номера верных утверждений.
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Вертикальные углы равны.
3) Любая биссектриса равнобедренного треугольника является его медианой.
Хочу получать новые решения
Ни какого спама
, или 
, где m - средняя линия трапеции. 
Автор: Таська
Комментарии: