Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах.
По свойству
равнобедренной трапеции - углы при основании равны.
Тогда /ADC=30°+45°=75°.
Сумма углов четырехугольника равна 360°, тогда получаем, что:
360°=75°+75°+/DCB+/CBA,
/DCB+/CBA=360°-75°-75°=210°, а учитывая, что /DCB=/CBA (по тому
свойству равнобедренной трапеции), получаем /DCB=/CBA=210°/2=105°, эти углы и есть бОльшие в трапеции
Ответ: 105
Поделитесь решением
Присоединяйтесь к нам...
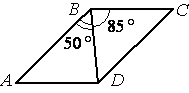Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
50° и 85°. Найдите меньший угол параллелограмма.
Углы при одном из оснований трапеции равны 48° и 42°, а отрезки, соединяющие середины противоположных сторон трапеции равны 6 и 3. Найдите основания трапеции.
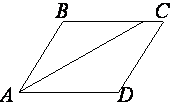Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 14°. Ответ дайте в градусах.
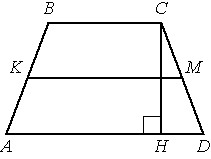В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 12, а меньшее основание BC равно 4.
Найдите площадь треугольника, изображённого на рисунке.
Хочу получать новые решения
Ни какого спама
, или 
, где m - средняя линия трапеции. 
Автор: Таська
Комментарии: