
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
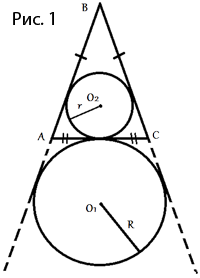 Проведем следующие отрезки (как показано на рисунке 2):
Проведем следующие отрезки (как показано на рисунке 2):
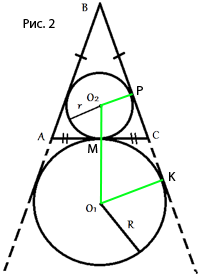 1) Из точки О2 к точке касания окружности и продолжения стороны ВС. (точка Р)
1) Из точки О2 к точке касания окружности и продолжения стороны ВС. (точка Р)
2) Из точки О1 к точке касания окружности и продолжения стороны ВС. (Точка К)
3) Из точки О1 к точке О2.
Заметим, что:
1) СМ=АС/2.
2) СР=СМ, по
второму свойству касательной.
3) СМ=СК, по
второму свойству касательной.
4) O1O2=R+r.
5) O2Р перпендикулярна AC, по
первому свойству касательной.
6) O1К тоже перпендикулярна AC, по
свойству касательной.
7) Из пунктов 2) и 3) следует, что СР=СК=СМ=АС/2. Тогда РК=АС/2+АС/2=АС.
Следовательно, O2Р ||
O1К (по
свойству параллельных прямых). Отсюда следует, что
О1О2РК - прямоугольная трапеция (по
определению трапеции).
Рассмотрим эту трапецию.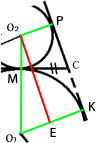
Проведем отрезок О2Е параллельный РК, а раз он параллелен РК, то в свою очередь перпендикулярен О1К и равен ему. Следовательно получившийся треугольник O1O2Е -
прямоугольный.
Тогда, по
теореме Пифагора, мы можем записать: (O1O2)2=(O2Е)2+(O1Е)2.
Подставим известные нам данные, полученные ранее:
(R+r)2=AC2+(R-r)2. Раскрываем скобки, получаем:
R2+2Rr+r2=AC2+R2-2Rr+r2
2Rr=AC2-2Rr
4Rr=AC2
r=(AC2)/4R
r=102/(4*8)
r=10*10/(4*8)
r=5*10/(2*8)
r=5*5/8
r=25/8
r=3,125
Ответ: радиус вписанной окружности равен 3,125.
Поделитесь решением
Присоединяйтесь к нам...
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=1:2, KM=23.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=1:2, KM=23.
 На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,6 м, если длина его тени равна 8 м, высота фонаря 5 м?
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,6 м, если длина его тени равна 8 м, высота фонаря 5 м?
 В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=88 и BC=BM. Найдите AH.
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=88 и BC=BM. Найдите AH.
 Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 15 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 8 м. Найдите длину троса.
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 15 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 8 м. Найдите длину троса.
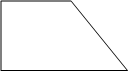 Тангенс острого угла прямоугольной трапеции равен 5/3. Найдите её большее основание, если меньшее основание равно высоте и равно 40.
Тангенс острого угла прямоугольной трапеции равен 5/3. Найдите её большее основание, если меньшее основание равно высоте и равно 40.

 , или
, или  , где m - средняя линия трапеции.
, где m - средняя линия трапеции.
Комментарии: