
Постройте график функции y=|x2-x-2|. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
Так как функция y=|x2-x-2| содержит
модуль, то данную функцию надо разложить на две функции, в зависимости от значения модуля.
 y=x2-x-2, при x2-x-2≥0
y=x2-x-2, при x2-x-2≥0
y=-(x2-x-2), при x2-x-2<0
Вычислим при каких значениях х функция меняет свой знак, для этого решим неравенство:
x2-x-2≥0
Найдем
корни уравнения x2-x-2=0
D=(-1)2-4*1*(-2)=1+8=9
x1=(-(-1)+3)/(2*1)=4/2=2
x2=(-(-1)-3)/(2*1)=-2/2=-1
 Решением данного неравенства будет диапазон (-∞; -1]∪[2; +∞), и меньше нуля в диапазоне (-1; 2).
Решением данного неравенства будет диапазон (-∞; -1]∪[2; +∞), и меньше нуля в диапазоне (-1; 2).
Значит можем переписать систему:
 y=x2-x-2, при x ∈ (-∞; -1]∪[2; +∞)
y=x2-x-2, при x ∈ (-∞; -1]∪[2; +∞)
y=-(x2-x-2), при x ∈ (-1; 2)
Построим оба графика по точкам:
1) y=x2-x-2, при x ∈ (-∞; -1]∪[2; +∞) (красный график):
| X | -3 | -2 | -1 | 2 | 3 | 4 |
| Y | 10 | 4 | 0 | 0 | 4 | 10 |
| X | -1 | 0 | 1 | 2 |
| Y | 0 | 2 | 2 | 0 |
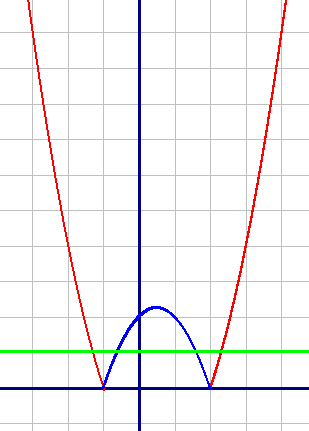 Очевидно, что прямая, параллельная оси абсцисс будет иметь максимум 4 общие точки. Это видно на примере зеленой прямой.
Очевидно, что прямая, параллельная оси абсцисс будет иметь максимум 4 общие точки. Это видно на примере зеленой прямой.Поделитесь решением
Присоединяйтесь к нам...
Найдите значение выражения 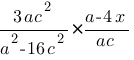 при a=2,1, c=-0,4.
при a=2,1, c=-0,4.
Решите уравнение (x2-25)2+(x2+3x-10)2=0.
Найдите значение выражения 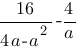 при a=-12.
при a=-12.
Какое из выражений равно степени 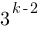 ?
?
1) 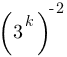
2) 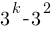
3) 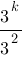
4) 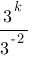
Какое из данных ниже чисел является значением выражения 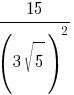
1) 1
2) 1/5
3) 1/3
4) 1/15
Комментарии: