ABCDEFGHIJ — правильный десятиугольник. Найдите угол CAH. Ответ дайте в градусах.
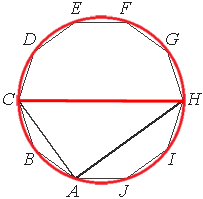Опишем окружность вокруг десятиугольника.
Заметим, что угол CAH является вписанным и опирается на дугу CDEFGH, которая равна 180°.
Следовательно ∠CAH=180°/2=90° (по
теореме о вписанном угле)
Ответ: 90
Поделитесь решением
Присоединяйтесь к нам...
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=12 и MB=18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=8, BF=15.
ABCDEFGHIJ — правильный десятиугольник. Найдите угол CAH. Ответ дайте в градусах.
Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Найдите площадь трапеции, изображённой на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: