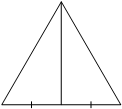
Медиана равностороннего треугольника равна 13√3. Найдите его сторону.
Вариант №1
По свойству равностороннего треугольника медиана равна (√3/2)*a, тогда:
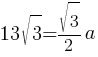
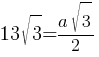
2*13√3=a√3
26√3=a√3
a=26
Ответ: 26
Поделитесь решением
Присоединяйтесь к нам...
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=27, CM=9. Найдите AO.
Укажите номера верных утверждений.
1) Любой квадрат является ромбом.
2) Против равных сторон треугольника лежат равные углы.
3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
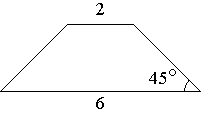В равнобедренной трапеции основания равны 2 и 6, а один из углов между боковой стороной и основанием равен
45°. Найдите площадь трапеции.
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 39°. Найдите величину угла OMK. Ответ дайте в градусах.
Площадь равнобедренного треугольника равна 196√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: