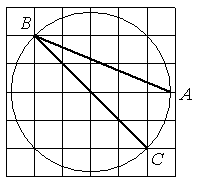
Найдите угол ABC. Ответ дайте в градусах.
Угол ABC (обозначим его α) является
вписанным в окружность, следовательно, он равен половине центрального угла, опирающегося на ту же дугу 2α (по
теореме).
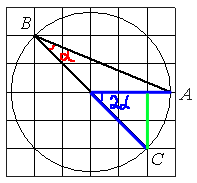Найдем
центральный угол через тангенс. Рассмотрим
центральный ("синий") угол и проведенный в нем катет ("зеленый").
tg(2α)=2/2=1
По
таблице угол 2α=45°
α=45°/2=22,5°
Ответ: 22,5
Поделитесь решением
Присоединяйтесь к нам...
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=79°. Найдите величину угла BOC. Ответ дайте в градусах.
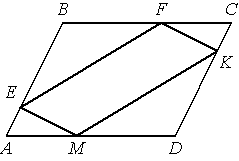В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём BF = DM, BE = DK. Докажите, что EFKM — параллелограмм.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 6. Найдите площадь трапеции.
Площадь прямоугольного треугольника равна
338√
В трапеции ABCD AB=CD, AC=AD и ∠ABC=123°. Найдите угол CAD. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: