На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что /NBA=11°. Найдите угол NMB. Ответ дайте в градусах.
Оговоримся сразу, рисунок несколько не соответствует условию задачи, на рисунке /NBA скорее равен 50°, поэтому не удивляйтесь, что будут расхождения с рисунком.
Угол NBA является
вписанным для данной окружности. Опирается этот угол на дугу AN. градусная мера дуги AN = /NBA*2=11°*2=22° (по
теореме о вписанном угле).
Градусная мера дуги ANB = 180° (т.к. AB - диаметр), следовательно, градусная мера дуги NB = дуга ANB - дуга AN = 180°-22°=158°
/NMB - тоже является
вписанным в окружность и равен половине градусной меры дуги NB (по
теореме).
/NMB=158°/2=79°
Ответ: /NMB=79°
Поделитесь решением
Присоединяйтесь к нам...
Радиус вписанной в квадрат окружности равен 22√2. Найдите диагональ этого квадрата.
Синус острого угла A треугольника ABC равен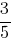 
. Найдите CosA.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=64°. Найдите угол NMB. Ответ дайте в градусах.
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 60, тангенс угла BAC равен 5/12. Найдите радиус окружности, вписанной в треугольник ABC.
Катеты прямоугольного треугольника равны 5√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: